Numeros complejos: INTRODUCCION A LOS NUMEROS COMPLEJOS

Los números complejos son una extensión de los números reales y forman el mínimo cuerpo algebraicamente cerrado que los contiene. El conjunto de los números complejos se designa como

, siendo

el conjunto de los reales se cumple que

. Los números complejos incluyen todas las raíces de los polinomios, a diferencia de los reales. Todo número complejo puede representarse como la suma de un número real y un número imaginario (que es un múltiplo real de la unidad imaginaria, que se indica con la letra i).

los números complejos se utilizan por doquier en matemáticas, en muchos campos de la física (notoriamente en la mecánica cuántica) y en ingeniería, especialmente en la electrónica y las telecomunicaciones, por su utilidad para representar las ondas electromagnéticas y la corriente eléctrica.

Definiremos cada complejo z como un par ordenado de números reales (a, b) ó (Re(z), Im(z)), en el que se definen las siguientes operaciones:

Suma

$(a, b) + (c, d) = (a+c,\, b+d)$

Producto por escalar

$r(a, b) = (ra,\, rb)$

Multiplicación

$(a, b) \cdot (c, d) = (ac - bd, ad + bc)$

Igualdad

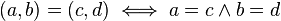
$(a, b) = (c, d) \iff a = c \and b = d$

A partir de estas operaciones podemos deducir otras como las siguientes:

Resta

$(a, b) - (c, d) = (a-c,\, b-d)$

División

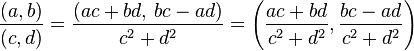
$\frac{(a, b)}{(c, d)} = {(ac+bd,\,bc-ad) \over c^2+d^2} = \left({ac + bd \over c^2 + d^2} , {bc - ad \over c^2 + d^2}\right)$

Para ampliar la información puedes vsitar NUMEROS COMPLEJOS EN EL PLANO CARTESIANO

Numeros complejos

hola

viernes, junio 28, 2013

INTRODUCCION A LOS NUMEROS COMPLEJOS

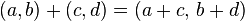
No hay comentarios:

Publicar un comentario