Aplicaciones
En matemáticas
Soluciones de ecuaciones polinómicas
Un raíz o cero del polinomio p es un complejo z tal que p(z)=0. Un resultado importante de esta definición es que todas las ecuaciones polinómicas (algebraicas) de grado n tienen exactamente n soluciones en el cuerpo de los números complejos, esto es, tiene exactamente n complejos z que cumplen la igualdad p(z)=0, contados con sus respectivas multiplicidades. También se cumple que si z es una raíz entonces su conjugado también es una raíz del polinomio p. A esto se lo conoce como Teorema Fundamental del Álgebra, y demuestra que los complejos son un cuerpo algebraicamente cerrado. Por esto los matemáticos consideran a los números complejos unos números más naturales que los números reales a la hora de resolver ecuaciones.Variable compleja o análisis complejo
Al estudio de las funciones de variable compleja se lo conoce como el Análisis complejo. Tiene una gran cantidad de usos como herramienta de matemáticas aplicadas
así como en otras ramas de las matemáticas. El análisis complejo provee
algunas importantes herramientas para la demostración de teoremas
incluso en teoría de números;
mientras que las funciones reales de variable real, necesitan de un
plano cartesiano para ser representadas; las funciones de variable
compleja necesitan un espacio de cuatro dimensiones, lo que las hace
especialmente difíciles de representar. Se suelen utilizar ilustraciones
coloreadas en un espacio de tres dimensiones para sugerir la cuarta
coordenada o animaciones en 3D para representar las cuatro.
Ecuaciones diferenciales
En ecuaciones diferenciales, cuando se estudian las soluciones de las ecuaciones diferenciales lineales con coeficientes constantes, es habitual encontrar primero las raíces (en general complejas)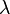
del polinomio característico, lo que permite expresar la solución general del sistema en términos de funciones de base de la forma: 
.En física
Los números complejos se usan en ingeniería electrónica y en otros campos para una descripción adecuada de las señales periódicas variables (ver Análisis de Fourier). En una expresión del tipo 
podemos pensar en 
como la amplitud y en 
como la fase de una onda sinusoidal de una frecuencia
dada. Cuando representamos una corriente o un voltaje de corriente
alterna (y por tanto con comportamiento sinusoidal) como la parte real
de una función de variable compleja de la forma 
donde ω representa la frecuencia angular y el número complejo z nos da la fase y la amplitud, el tratamiento de todas las fórmulas que rigen las resistencias, capacidades e inductores pueden ser unificadas introduciendo resistencias imaginarias para las dos últimas (ver redes eléctricas). Ingenieros eléctricos y físicos usan la letra j para la unidad imaginaria en vez de i que está típicamente destinada a la intensidad de corriente.
podemos pensar en como la amplitud y en como la fase de una onda sinusoidal de una frecuencia
dada. Cuando representamos una corriente o un voltaje de corriente
alterna (y por tanto con comportamiento sinusoidal) como la parte real
de una función de variable compleja de la forma donde ω representa la frecuencia angular y el número complejo z nos da la fase y la amplitud, el tratamiento de todas las fórmulas que rigen las resistencias, capacidades e inductores pueden ser unificadas introduciendo resistencias imaginarias para las dos últimas (ver redes eléctricas). Ingenieros eléctricos y físicos usan la letra j para la unidad imaginaria en vez de i que está típicamente destinada a la intensidad de corriente.
El campo complejo es igualmente importante en mecánica cuántica cuya matemática subyacente utiliza Espacios de Hilbert de dimensión infinita sobre C (ℂ).
En la relatividad especial y la relatividad general, algunas fórmulas para la métrica del espacio-tiempo son mucho más simples si tomamos el tiempo como una variable imaginaria.
GRACIAS POR SU VISITA, para iniciar el recorrido haga click en el siguiente enlace: comienzo
No hay comentarios:
Publicar un comentario